Norton’s Theorem

Norton’s theorem is used to simplify complex linear circuits and making circuit analysis easy and fast. This theorem was proposed by E. L. Norton, an American engineer at Bell Laboratories. He came up with a new approach to simplify complex circuits containing several voltage sources, current sources and resistors with two terminals.

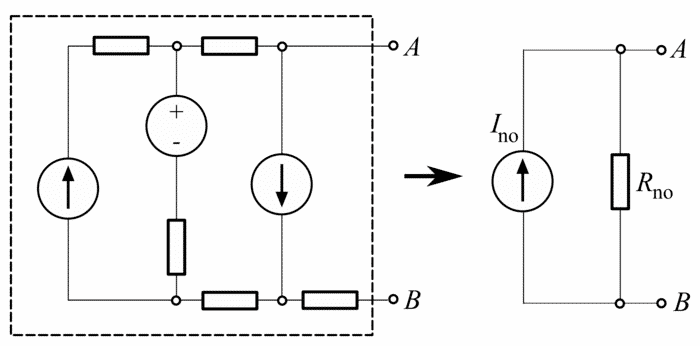
Norton’s theorem is somewhat similar to Thevenin’s Theorem. It can simplify any complex circuits to a single resistance in parallel with a constant current source.   

Norton’s theorem statement

Norton’s theorem states that a linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source I_N in parallel with a resistor R_N, where I_N is the short-circuit current through the terminals and R_N is the input or equivalent resistance at the terminals when the independent sources are turned off.

Verification of Norton’s theorem

Let’s find Norton’s equivalent circuit for the below circuit. Then verify the current flow through the load resistance 5Ω in original circuit and the simplified circuit.

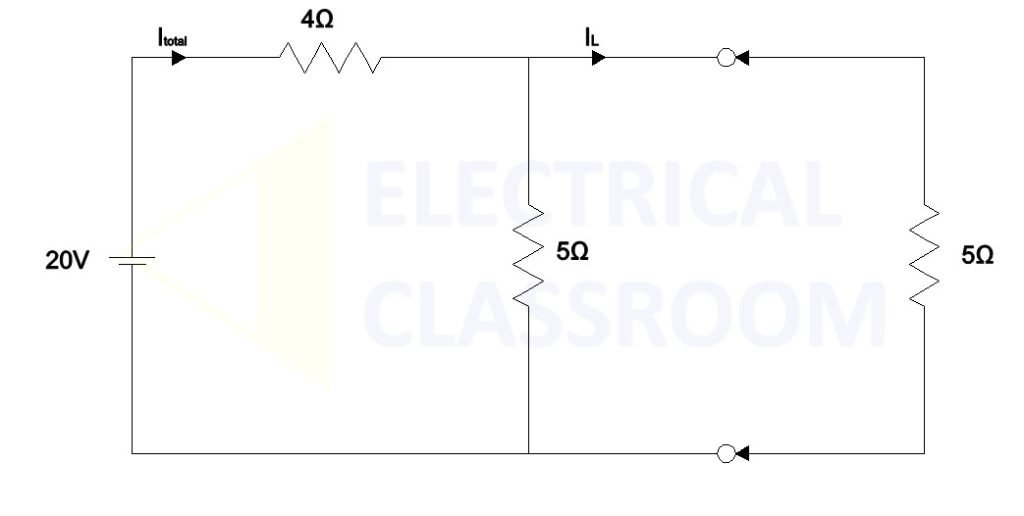
The equivalent resistance offered by the above circuit when is

R_total   = 4 + 5||5 = 4 + 5 x 5 / 5+5 = 4 + 25/10 = 4 + 2.5 = 7.5Ω

Total current flow

I_total   = 20V / 6.5 Ω = 3.08A

Now we can calculate the current flow I_L through the load resistance using the current division rule.

I_L = 2.667 X 5 /10 = 1.54A ————-[1]

Now let us find the Norton’s equivalent circuit and calculate the current flow through the load resistance. As said before Norton’s equivalent circuit consists of a current source, I_Norton (known as Norton’s current) in parallel to resistance, R_Norton (known as Norton’s equivalent resistance). To find Norton’s current,  I_Norton, remove the load resistance and directly short the load terminals.

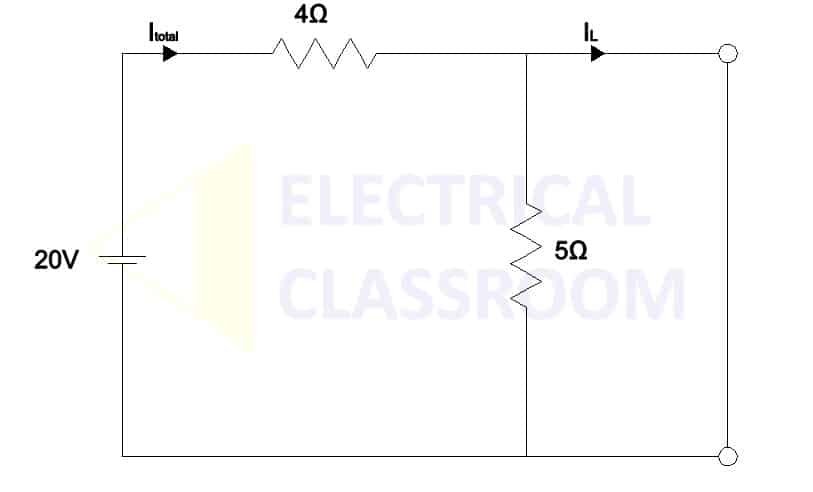
Norton’s current, I_Norton = 20V / 4Ω = 5A

Find the Norton’s resistance

To find Norton’s resistance, R_Norton, all voltage sources must be turned off, meaning it acts like a short circuit and all current sources act like an open circuit, as shown in the figure below:

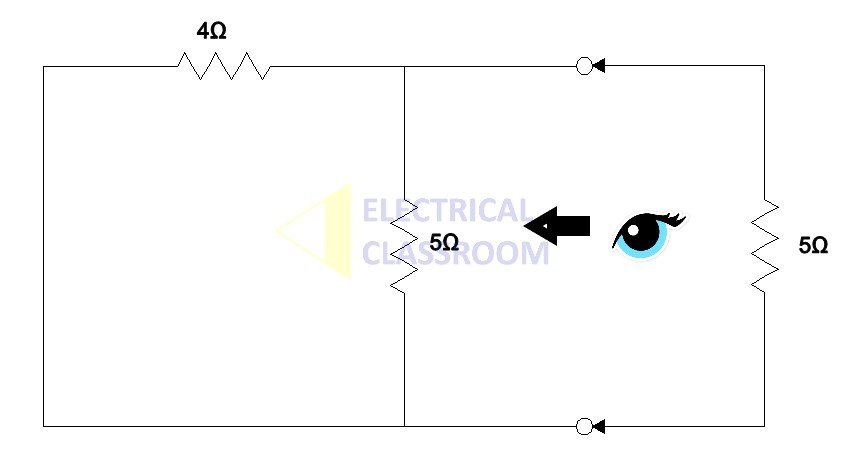
Norton’s resistance, R_Norton = 5|| 4 = 2.22 Ω

Norton’s equivalent circuit:

Using I_Norton and R_Norton now we can form Norton’s equivalent circuit:

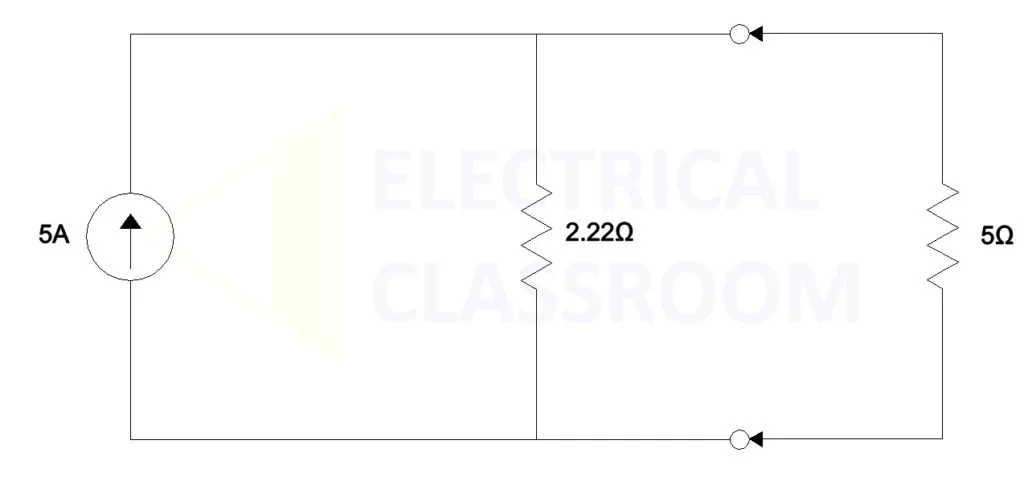
Now let us calculate the current flow through the load resistance,

I_L = 5 X 2.22 / 7.22 = 1.54A ————-[2]

From equation [1] and [2], it is proved that the current flow and through the load resistance remains same in the original circuit and the Norton’s equivalent circuit.

Summary

Steps to find Norton’s equivalent circuit:

• Calculate the Norton’s current by removing the load resistance and directly short the load terminals.
• Calculate the Norton’s equivalent resistance by turning off voltage sources and removing current sources.
• Draw a circuit with Norton’s current source in parallel with the equivalent resistance and load resistance connected between its terminals.
• Now calculate the current flow through and the voltage measured across the load resistance.